Today's PUZZLE CLASSIC OF THE DAY
PREVIOUS 12 DAYS
Birdie: 2 Congruent Parts
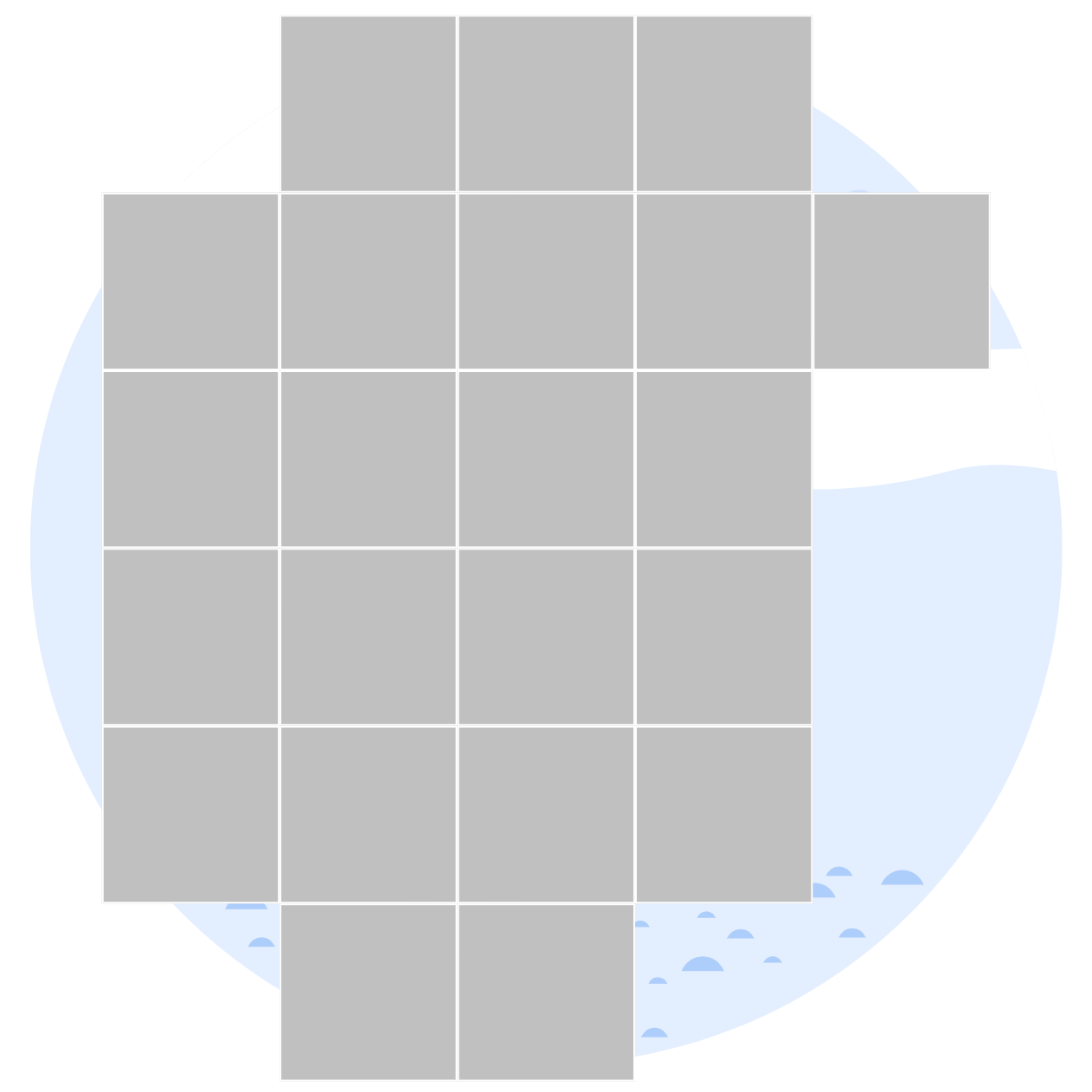
Cut this figure into 2 congruent parts (identical in area and shape, though they can be mirrored).
TriCounting: Cubic Lattice

How many triangles are in this figure? Select a triangle and click the "Count" button.
TriCounting: Triangle Cones

How many triangles are in this figure? Select a triangle and click the "Count" button.
Grinder: 2 Congruent Parts
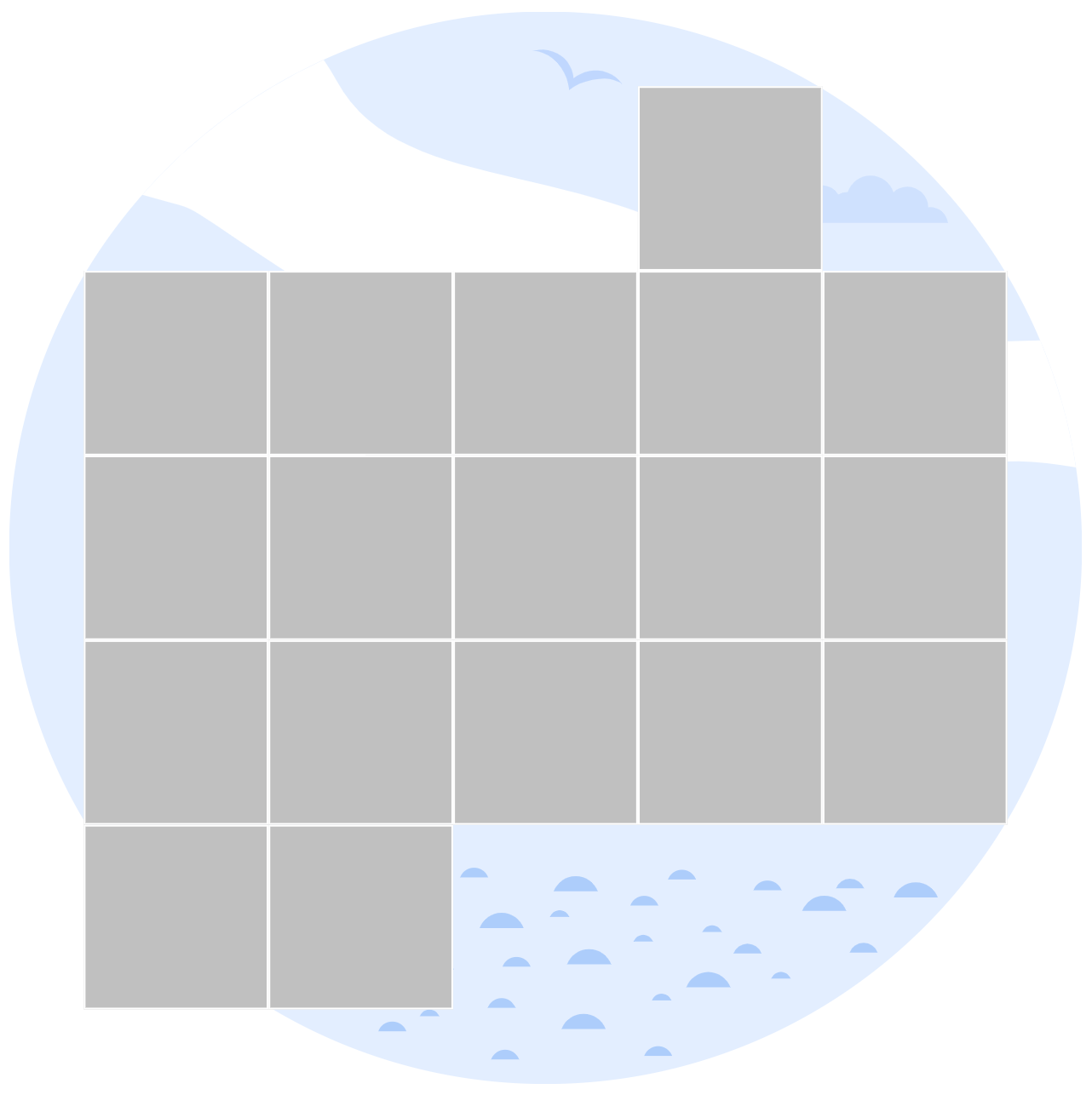
Cut this figure into 2 congruent parts (identical in area and shape, though they can be mirrored).
What Day?
If two days ago was the day preceding Tuesday, what day will be the day after tomorrow?
Age of Spouses
A married woman states: "My husband's age is a two-digit number, which, when digits are swapped, gives my age. He is older than me and our age difference is 1/11th of our ages' sum." How old are the spouses?
Four 5's to 16

Using some arithmetic operations, convert four 5's into 16.
Cutout & Hole: 2 Congruent Parts
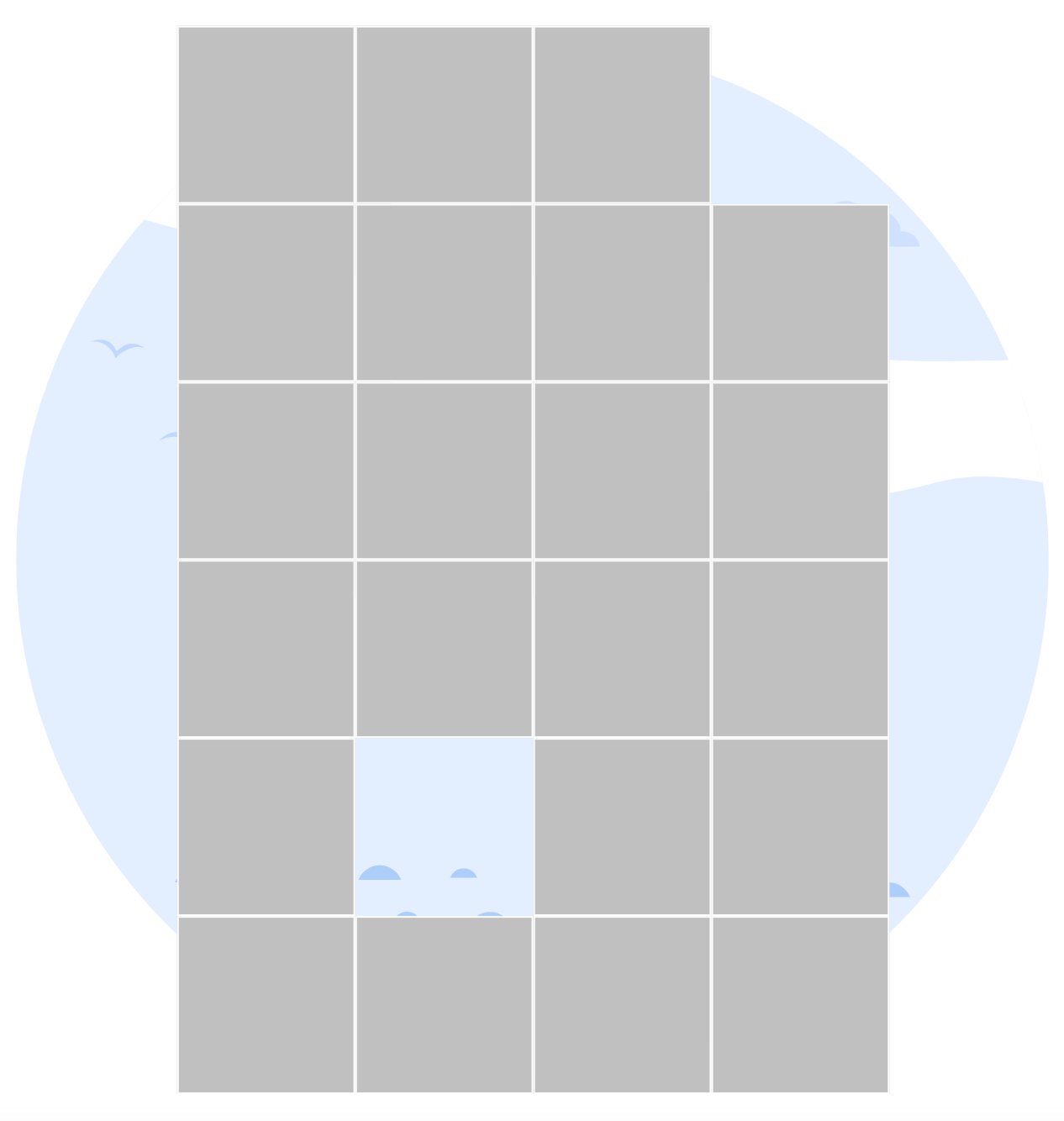
Cut this figure into 2 congruent parts (identical in area and shape, though they can be mirrored).
Spiral: 2 Congruent Parts

Cut this figure into 2 congruent parts (identical in area and shape).
TriCounting: 5 Rotating Squares

How many triangles are in this figure? Select a triangle and click the "Count" button.
Circle Relationship
One circle is circumscribed around a square. Another circle is inscribed within the same square. Using 2's and r's, show the ratio between the circles' areas.
TriCounting: M in Triangle

How many triangles are in this figure? Select a triangle and click the "Count" button.
