Today's PUZZLE CLASSIC OF THE DAY
PREVIOUS 12 DAYS
Send More Money

Each letter represents a different digit, and M is not zero. Replace the letters with the respective digits to restore a valid expression.
Twice Older, Twice Younger
A young woman is twice older than her brother, and twice as young as her father. In 22 years not her, but her brother will be twice as young as their father. How old is each of them now?
Eight Stars in a Circle

Divide the circle into 4 areas, of the same shape and size, each containing TWO stars.
From 1 to 100
There is quite a prompt way to calculate a total of all the numbers from 1 to 100. Can you, using only 0's and 1's, fill in the gaps in the formula to reach the total?
Ice Cream into 6 Congruent Parts

Cut this ice-cream-like shape into six congruent parts, each of which would contain a strawberry.
Tower Clock's Magical Dial
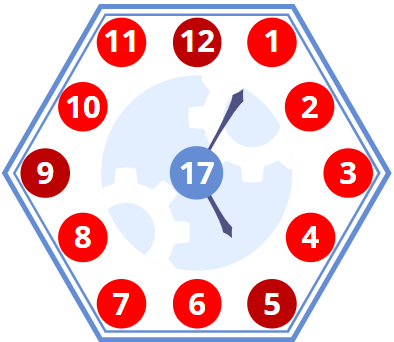
An unusual hexagon-shaped clock has been installed on a city hall tower. It happened to have an interesting feature. It is possible to rearrange its numbers in such a way that the total along each side is 17. Can you achieve this, knowing 12, 5, and 9 remain unmoved?
4 Screws - 4 Parts
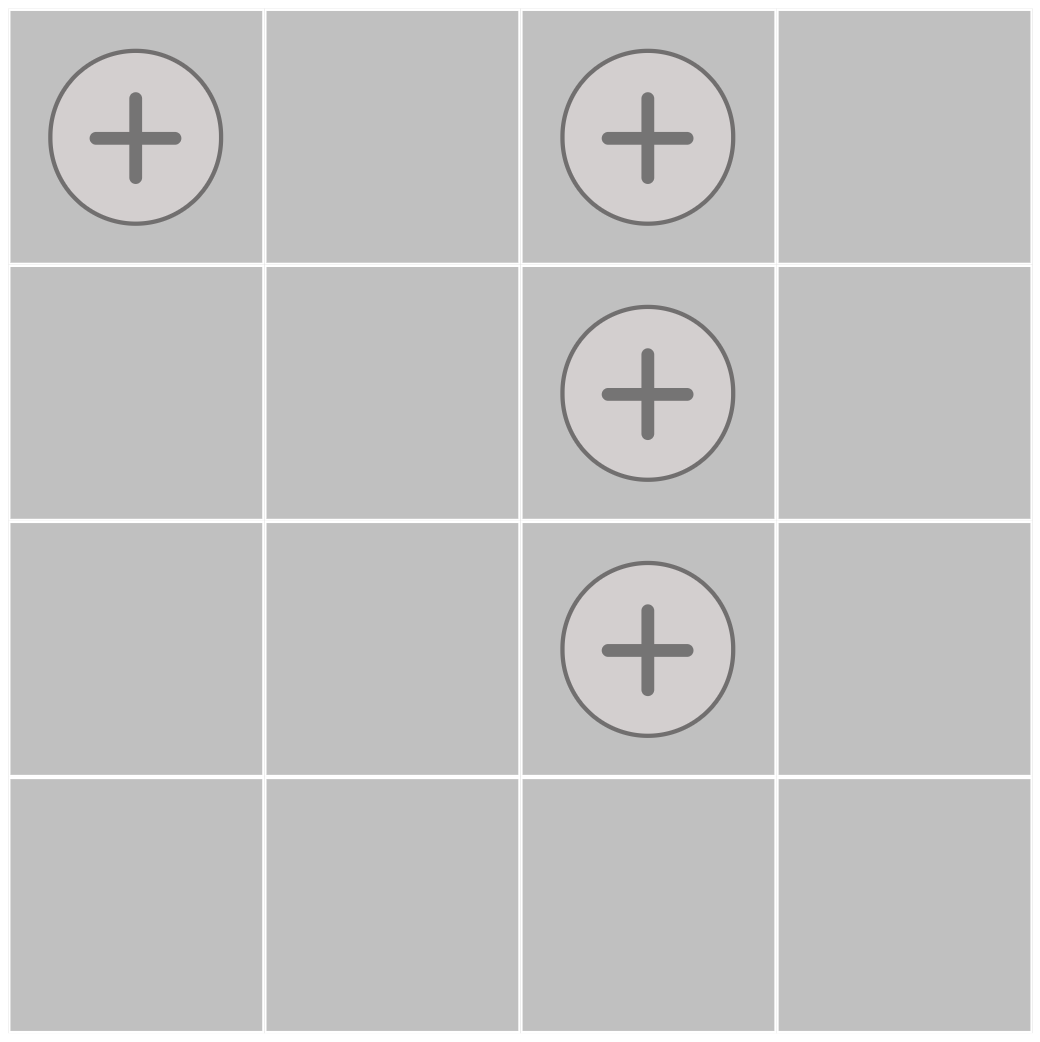
Cut this square plate into four congruent parts, each of which would contain a screw.
Playing Cards' Magic Square
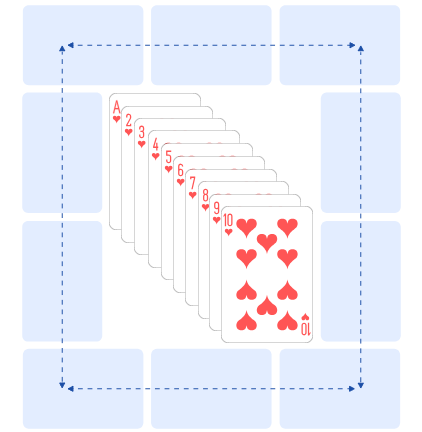
Place ten playing cards, from Ace to 10 (Ace counting as 1) into the cells of this square frame, so that the cards' values along each of the four sides of the frame add up to 18.
2, 3, 4, 5 to a Valid Equation
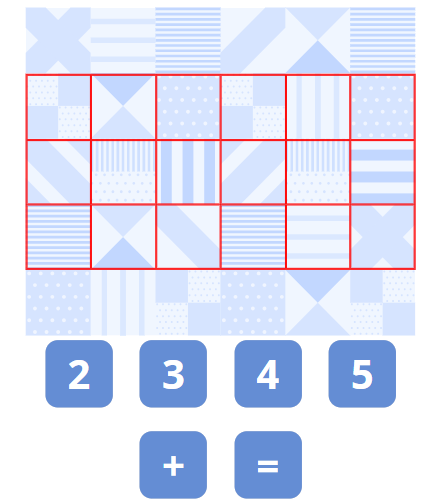
Place digits 2, 3, 4, 5 and signs "+" and "=" somewhere in the grid so that to get a valid equation.
Star Strips

Rearrange the strips so that a perfect six-pointed star would appear. In the correct composition the strips will change their color into green.
Square 5x5 into 4x4 and 3x3 Squares
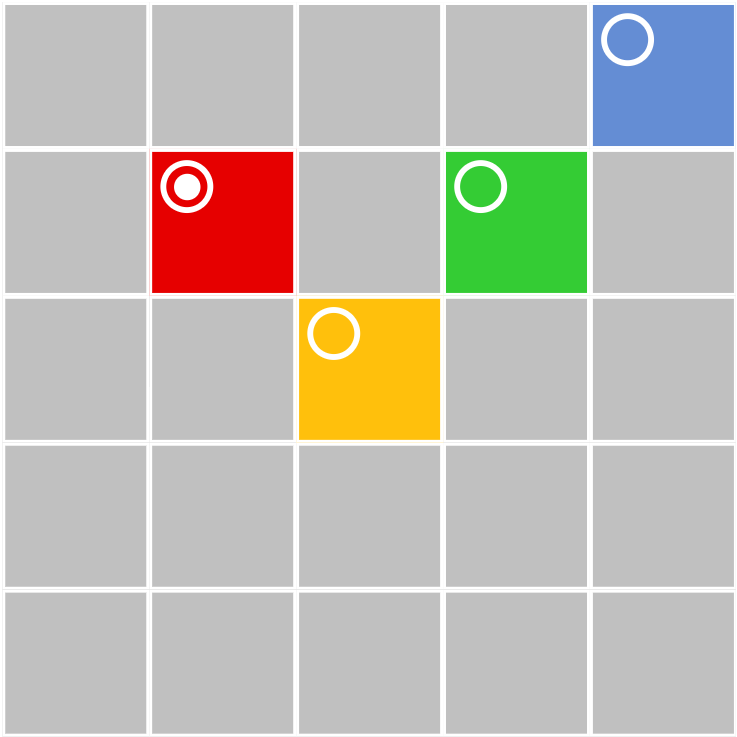
Cut the 5x5 square into 4 rectangular parts which would make a 4x4 and a 3x3 square when rearranged.
4 Rays in Triangle: Counting Triangles
How many triangles can you count here?

